-
Notifications
You must be signed in to change notification settings - Fork 147
Dec 29, 2020
This programming exercise instruction was originally developed and written by Prof. Andrew Ng as part of his machine learning course on Coursera platform. I have adapted the instruction for R language, so that its users, including myself, could also take and benefit from the course.
In this exercise, you will implement logistic regression and apply it to
two different datasets. Before starting on the programming exercise, we
strongly recommend watching the video lectures and completing the review
questions for the associated topics. To get started with the exercise,
you will need to download the starter code and unzip its contents to the
directory where you wish to complete the exercise. If needed, use the
setwd() function in R to change to this directory before starting this
exercise.
Files included in this exercise:
-
ex3.R- R script that steps you through part 1 -
ex3_nn.R- R script that steps you through part 2 -
ex3data1.Rda- Training set of hand-written digits -
ex3weights.Rda- Initial weights for the neural network exercise -
submit.R- Submission script that sends your solutions to our servers -
displayData.R- Function to help visualize the dataset -
sigmoid.R- Sigmoid function - [⋆]
lrCostFunction.R- Logistic regression cost function - [⋆]
oneVsAll.R- Train a one-vs-all multi-class classifier - [⋆]
predictOneVsAll.R- Predict using a one-vs-all multi-class classifier - [⋆]
predict.R- Neural network prediction function
⋆ indicates files you will need to complete
Throughout the exercise, you will be using the scripts ex3.R and
ex3_nn.R. These scripts set up the dataset for the problems and make
calls to functions that you will write. You do not need to modify these
scripts. You are only required to modify functions in other files, by
following the instructions in this assignment.
The exercises in this course use R, a high-level programming language
well-suited for numerical computations. If you do not have R installed,
please download a Windows installer from
R-project website.
R-Studio is a free and
open-source R integrated development environment (IDE) making R script
development a bit easier when compared to the R’s own basic GUI. You may
start from the .Rproj (a R-Studio project file) in each exercise
directory. At the R command line, typing help followed by a function
name displays documentation for that function. For example,
help('plot') or simply ?plot will bring up help information for
plotting. Further documentation for R functions can be found at the R
documentation pages.
For this exercise, you will use logistic regression and neural networks to recognize handwritten digits (from 0 to 9). Automated handwritten digit recognition is widely used today - from recognizing zip codes (postal codes) on mail envelopes to recognizing amounts written on bank checks. This exercise will show you how the methods you’ve learned can be used for this classification task. In the first part of the exercise, you will extend your previous implemention of logistic regression and apply it to one-vs-all classification.
You are given a data set in ex3data1.Rda that contains 5000 training
examples of handwritten digits.[1] The .Rda format means that that
the data has been saved in a native R matrix format, instead of a text
(ASCII) format like a csv-file. These matrices can be read directly into
your program by using the load function. After loading, matrices of
the correct dimensions and values will appear in your program’s memory.
The matrices will already be named as elements of the data list.
list2env function defines them in R’s global environment for
convenience and is wrapped in invisible function to prevent the
printing of the returned object. Finally, rm function removes the
data object.
# load X and y matrices into the global environment
load('ex3data1.Rda')There are 5000 training examples in ex3data1.Rda, where each training
example is a 20 pixel by 20 pixel grayscale image of the digit. Each
pixel is represented by a floating point number indicating the grayscale
intensity at that location. The 20 by 20 grid of pixels is “unrolled”
into a 400-dimensional vector. Each of these training examples becomes a
single row in our data matrix X. This gives us a 5000 by 400 matrix X
where every row is a training example for a handwritten digit image.

The second part of the training set is a 5000-dimensional vector y that contains labels for the training set. To make things more compatible with R indexing, where there is no zero index, we have mapped the digit zero to the value ten. Therefore, a “0” digit is labeled as “10”, while the digits “1” to “9” are labeled as “1” to “9” in their natural order.
You will begin by visualizing a subset of the training set. In Part 1 of
ex3.R, the code randomly selects 100 rows from X and passes those rows
to the displayData function. This function maps each row to a 20 pixel
by 20 pixel grayscale image and displays the images together. We have
provided the displayData function, and you are encouraged to examine
the code to see how it works. After you run this step, you should see an
image like Figure 1.

Figure 1: Examples from the dataset
You will be using multiple one-vs-all logistic regression models to build a multi-class classifier. Since there are 10 classes, you will need to train 10 separate logistic regression classifiers. To make this training efficient, it is important to ensure that your code is well vectorized. In this section, you will implement a vectorized version of logistic regression that does not employ any for loops. You can use your code in the last exercise as a starting point for this exercise.
We will begin by writing a vectorized version of the cost function. Recall that in (unregularized) logistic regression, the cost function is

To compute each element in the summation, we have to compute
 for every example i, where
for every example i, where 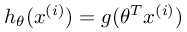 and
and  is the sigmoid function. It turns out that
we can compute this quickly for all of our examples by using matrix
multiplication. Let us define X and
is the sigmoid function. It turns out that
we can compute this quickly for all of our examples by using matrix
multiplication. Let us define X and 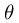 as
as

Then, by computing the matrix product  , we have
, we have

In the last equality, we used the fact that  if
if
 and
and  are vectors. This
allows us to compute the products
are vectors. This
allows us to compute the products  for all our
examples
for all our
examples  in one line of code. Your job is to
write the unregularized cost function in the file
in one line of code. Your job is to
write the unregularized cost function in the file lrCostFunction.R.
Your implementation should use the strategy we presented above to
calculate  . You should also use a vectorized
approach for the rest of the cost function. A fully vectorized version
of
. You should also use a vectorized
approach for the rest of the cost function. A fully vectorized version
of lrCostFunction.R should not contain any loops. (Hint: You might
want to use the element-wise multiplication operation (*) and the sum
operation sum when writing this function)
Recall that the gradient of the (unregularized) logistic regression cost
is a vector where the  element is defined as
element is defined as
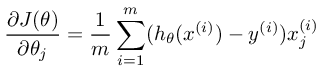
To vectorize this operation over the dataset, we start by writing out
all the partial derivatives explicitly for all 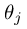 ,
,

where

Note that  is a vector, while
is a vector, while
 is a scalar (single number). To understand the
last step of the derivation, let
is a scalar (single number). To understand the
last step of the derivation, let  and observe
that:
and observe
that:

where the values 
The expression above allows us to compute all the partial derivatives
without any loops. If you are comfortable with linear algebra, we
encourage you to work through the matrix multiplications above to
convince yourself that the vectorized version does the same
computations. You should now implement Equation 1 to compute the correct
vectorized gradient. Once you are done, complete the function
lrCostFunction.R by implementing the gradient.
Debugging Tip: Vectorizing code can sometimes be tricky. One common
strategy for debugging is to print out the sizes of the matrices you are
working with using the size function. For example, given a data matrix
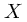 of size
of size  (100 examples, 20
features) and
(100 examples, 20
features) and 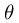 , a vector with dimensions
, a vector with dimensions
 , you can observe that
, you can observe that  is
a valid multiplication operation, while
is
a valid multiplication operation, while  is not.
Furthermore, if you have a non-vectorized version of your code, you can
compare the output of your vectorized code and non-vectorized code to
make sure that they produce the same outputs.
is not.
Furthermore, if you have a non-vectorized version of your code, you can
compare the output of your vectorized code and non-vectorized code to
make sure that they produce the same outputs.
After you have implemented vectorization for logistic regression, you will now add regularization to the cost function. Recall that for regularized logistic regression, the cost function is defined as
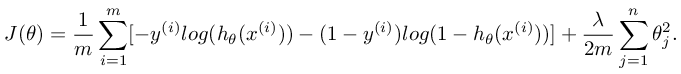
Note that you should not be regularizing  which
is used for the bias term. Correspondingly, the partial derivative of
regularized logistic regression cost for
which
is used for the bias term. Correspondingly, the partial derivative of
regularized logistic regression cost for 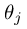 is
defined as
is
defined as

Now modify your code in lrCostFunction to account for regularization.
Once again, you should not put any loops into your code.
R Tip: When implementing the vectorization for regularized logistic
regression, you might often want to only sum and update certain elements
of 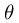 . In R, you can index into the matrices to
access and update only certain elements. For example,
. In R, you can index into the matrices to
access and update only certain elements. For example, A[, 3:5] <- B[, 1:3] will replace the columns 3 to 5 of A with the columns 1 to 3
from B. Negative values could be used in indexing. This allows us to
exclude columns (or rows) from the matrix. For example, A[, -1] will
only return elements from the  to last column of
A. Thus, you could use this together with the
to last column of
A. Thus, you could use this together with the sum and ^ operations
to compute the sum of only the elements you are interested in (e.g.,
sum(z[-1]^2)). In the starter code, lrCostFunction.R, we have also
provided hints on yet another possible method for computing the
regularized gradient.
You should now submit your solutions.
In this part of the exercise, you will implement one-vs-all
classification by training multiple regularized logistic regression
classifiers, one for each of the K classes in our dataset (Figure 1). In
the handwritten digits dataset,  , but your code
should work for any value of K. You should now complete the code in
, but your code
should work for any value of K. You should now complete the code in
oneVsAll.R to train one classifier for each class. In particular, your
code should return all the classifier parameters in a matrix
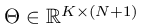 , where each row of
, where each row of 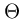 corresponds to the learned logistic regression parameters for one class.
You can do this with a for loop from 1 to K, training each classifier
independently. Note that the y argument to this function is a vector of
labels from 1 to 10, where we have mapped the digit 0 to the label 10
(to avoid confusions with indexing). When training the classifier for
class
corresponds to the learned logistic regression parameters for one class.
You can do this with a for loop from 1 to K, training each classifier
independently. Note that the y argument to this function is a vector of
labels from 1 to 10, where we have mapped the digit 0 to the label 10
(to avoid confusions with indexing). When training the classifier for
class  , you will want a m-dimensional vector of
labels y, where
, you will want a m-dimensional vector of
labels y, where  , 1 indicates whether the
, 1 indicates whether the
 training instance belongs to class
training instance belongs to class
 , or if it belongs to a different class
, or if it belongs to a different class
 . You may find logical arrays helpful for this
task.
. You may find logical arrays helpful for this
task.
R Tip: Logical arrays in R are arrays which contain binary (TRUE or
FALSE) elements. In R, evaluating the expression a==b for a vector a
(of size 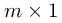 ) and scalar
) and scalar b will return a vector of
the same size as a with TRUE at positions where the elements of a
are equal to b and FALSE where they are different. To see how this
works for yourself, try the following code in R:
a = 1:10
b = 3
# You should try different values of b here
a == b## [1] FALSE FALSE TRUE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
After you have correctly completed the code for oneVsAll.R, the script
ex3.R will continue to use your oneVsAll function to train a
multi-class classifier.
You should now submit your solutions.
After training your one-vs-all classifier, you can now use it to predict
the digit contained in a given image. For each input, you should compute
the probability that it belongs to each class using the trained logistic
regression classifiers. Your one-vs-all prediction function will pick
the class for which the corresponding logistic regression classifier
outputs the highest probability and return the class label
 as the prediction for the input example. You
should now complete the code in
as the prediction for the input example. You
should now complete the code in predictOneVsAll.R to use the
one-vs-all classifier to make predictions. Once you are done, ex3.R
will call your predictOneVsAll function using the learned value of
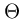 . You should see that the training set accuracy
is about 94.9% (i.e., it classifies 94.9% of the examples in the
training set correctly).
. You should see that the training set accuracy
is about 94.9% (i.e., it classifies 94.9% of the examples in the
training set correctly).
You should now submit your solutions.
In the previous part of this exercise, you implemented multi-class logistic regression to recognize handwritten digits. However, logistic regression cannot form more complex hypotheses as it is only a linear classifier.[2]
In this part of the exercise, you will implement a neural network to
recognize handwritten digits using the same training set as before. The
neural network will be able to represent complex models that form
non-linear hypotheses. For this week, you will be using parameters from
a neural network that we have already trained. Your goal is to implement
the feedforward propagation algorithm to use our weights for prediction.
In next week’s exercise, you will write the backpropagation algorithm
for learning the neural network parameters. The provided script,
ex3_nn.R, will help you step through this exercise.
Our neural network is shown in Figure 2. It has 3 layers – an input
layer, a hidden layer and an output layer. Recall that our inputs are
pixel values of digit images. Since the images are of size
 , this gives us 400 input layer units (excluding
the extra bias unit which always outputs +1). As before, the training
data will be loaded into the variables
, this gives us 400 input layer units (excluding
the extra bias unit which always outputs +1). As before, the training
data will be loaded into the variables 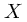 and
and
 . You have been provided with a set of network
parameters
. You have been provided with a set of network
parameters  already trained by us. These are
stored in
already trained by us. These are
stored in ex3weights.Rda and will be loaded by ex3_nn.R into
Theta1 and Theta2. The parameters have dimensions that are sized for
a neural network with 25 units in the second layer and 10 output units
(corresponding to the 10 digit classes).
# Load the matrices Theta1 and Theta2 in your R global environment
# Theta1 has size 25 x 401
# Theta2 has size 10 x 26
load('ex3weights.Rda')
Figure 2: Neural network model.
Now you will implement feedforward propagation for the neural network.
You will need to complete the code in predict.R to return the neural
network’s prediction. You should implement the feedforward computation
that computes  for every example
for every example
 and returns the associated predictions. Similar
to the one-vs-all classification strategy, the prediction from the
neural network will be the label that has the largest output
and returns the associated predictions. Similar
to the one-vs-all classification strategy, the prediction from the
neural network will be the label that has the largest output
 .
.
Implementation Note: The matrix X contains the examples in rows.
When you complete the code in predict.R, you will need to add the
column of 1’s to the matrix. The matrices Theta1 and Theta2 contain
the parameters for each unit in rows. Specifically, the first row of
Theta1 corresponds to the first hidden unit in the second layer. In R,
when you compute  , be sure that you index (and if
necessary, transpose)
, be sure that you index (and if
necessary, transpose) 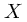 correctly so that you get
correctly so that you get
 as a column vector.
as a column vector.
Once you are done, ex3_nn.R will call your predict function using the
loaded set of parameters for Theta1 and Theta2. You should see that
the accuracy is about 97.5%. After that, an interactive sequence will
launch displaying images from the training set one at a time, while the
console prints out the predicted label for the displayed image. To stop
the image sequence, press Ctrl-C.
You should now submit your solutions.
After completing this assignment, be sure to use the submit function to sub- mit your solutions to our servers. The following is a breakdown of how each part of this exercise is scored.
| Part | Submitted File | Points |
|---|---|---|
| Regularized Logisic Regression | lrCostFunction.R |
30 points |
| One-vs-all classifier training | oneVsAll.R |
20 points |
| One-vs-all classifier prediction | predictOneVsAll.R |
20 points |
| Neural Network Prediction Function | predict.R |
30 points |
| Total Points | 100 points |
You are allowed to submit your solutions multiple times, and we will take only the highest score into consideration.
-
This is a subset of the MNIST handwritten digit dataset (http://yann.lecun.com/exdb/mnist/).
-
You could add more features (such as polynomial features) to logistic regression, but that can be very expensive to train.