-
Notifications
You must be signed in to change notification settings - Fork 4
Commit
This commit does not belong to any branch on this repository, and may belong to a fork outside of the repository.
- Loading branch information
Showing
5 changed files
with
214 additions
and
0 deletions.
There are no files selected for viewing
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
| Original file line number | Diff line number | Diff line change |
|---|---|---|
| @@ -0,0 +1,81 @@ | ||
| # 963. Minimum Area Rectangle II | ||
| You are given an array of points in the **X-Y** plane `points` where <code>points[i] = [x<sub>i</sub>, y<sub>i</sub>]</code>. | ||
|
|
||
| Return *the minimum area of any rectangle formed from these points, with sides **not necessarily parallel** to the X and Y axes*. If there is not any such rectangle, return `0`. | ||
|
|
||
| Answers within <code>10<sup>-5</sup></code> of the actual answer will be accepted. | ||
|
|
||
| #### Example 1: | ||
|  | ||
| <pre> | ||
| <strong>Input:</strong> points = [[1,2],[2,1],[1,0],[0,1]] | ||
| <strong>Output:</strong> 2.00000 | ||
| <strong>Explanation:</strong> The minimum area rectangle occurs at [1,2],[2,1],[1,0],[0,1], with an area of 2. | ||
| </pre> | ||
|
|
||
| #### Example 2: | ||
|  | ||
| <pre> | ||
| <strong>Input:</strong> points = [[0,1],[2,1],[1,1],[1,0],[2,0]] | ||
| <strong>Output:</strong> 1.00000 | ||
| <strong>Explanation:</strong> The minimum area rectangle occurs at [1,0],[1,1],[2,1],[2,0], with an area of 1. | ||
| </pre> | ||
|
|
||
| #### Example 3: | ||
|  | ||
| <pre> | ||
| <strong>Input:</strong> points = [[0,3],[1,2],[3,1],[1,3],[2,1]] | ||
| <strong>Output:</strong> 0 | ||
| <strong>Explanation:</strong> There is no possible rectangle to form from these points. | ||
| </pre> | ||
|
|
||
| #### Constraints: | ||
| * `1 <= points.length <= 50` | ||
| * `points[i].length == 2` | ||
| * <code>0 <= x<sub>i</sub>, y<sub>i</sub> <= 4 * 10<sup>4</sup></code> | ||
| * All the given points are **unique**. | ||
|
|
||
| ## Solutions (Rust) | ||
|
|
||
| ### 1. Solution | ||
| ```Rust | ||
| use std::collections::HashSet; | ||
|
|
||
| impl Solution { | ||
| pub fn min_area_free_rect(points: Vec<Vec<i32>>) -> f64 { | ||
| let points_set = points.iter().map(|p| (p[0], p[1])).collect::<HashSet<_>>(); | ||
| let mut ret = f64::NAN; | ||
|
|
||
| for i in 0..points.len() { | ||
| let (xi, yi) = (points[i][0], points[i][1]); | ||
|
|
||
| for j in i + 1..points.len() { | ||
| let (xj, yj) = (points[j][0], points[j][1]); | ||
| let ij2 = (xi - xj).pow(2) as f64 + (yi - yj).pow(2) as f64; | ||
|
|
||
| for k in j + 1..points.len() { | ||
| let (xk, yk) = (points[k][0], points[k][1]); | ||
| let ik2 = (xi - xk).pow(2) as f64 + (yi - yk).pow(2) as f64; | ||
| let jk2 = (xj - xk).pow(2) as f64 + (yj - yk).pow(2) as f64; | ||
|
|
||
| if ij2 + ik2 == jk2 && points_set.contains(&(xj + xk - xi, yj + yk - yi)) { | ||
| ret = ret.min(ij2.sqrt() * ik2.sqrt()); | ||
| } else if ij2 + jk2 == ik2 && points_set.contains(&(xi + xk - xj, yi + yk - yj)) | ||
| { | ||
| ret = ret.min(ij2.sqrt() * jk2.sqrt()); | ||
| } else if ik2 + jk2 == ij2 && points_set.contains(&(xi + xj - xk, yi + yj - yk)) | ||
| { | ||
| ret = ret.min(ik2.sqrt() * jk2.sqrt()); | ||
| } | ||
| } | ||
| } | ||
| } | ||
|
|
||
| if ret.is_nan() { | ||
| return 0.; | ||
| } | ||
|
|
||
| ret | ||
| } | ||
| } | ||
| ``` |
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
| Original file line number | Diff line number | Diff line change |
|---|---|---|
| @@ -0,0 +1,88 @@ | ||
| # 963. 最小面积矩形 II | ||
| 给定在 xy 平面上的一组点,确定由这些点组成的任何矩形的最小面积,其中矩形的边**不一定平行于** x 轴和 y 轴。 | ||
|
|
||
| 如果没有任何矩形,就返回 0。 | ||
|
|
||
| #### 示例 1: | ||
|  | ||
| <pre> | ||
| <strong>输入:</strong> points = [[1,2],[2,1],[1,0],[0,1]] | ||
| <strong>输出:</strong> 2.00000 | ||
| <strong>解释:</strong> 最小面积的矩形出现在 [1,2],[2,1],[1,0],[0,1] 处,面积为 2。 | ||
| </pre> | ||
|
|
||
| #### 示例 2: | ||
|  | ||
| <pre> | ||
| <strong>输入:</strong> points = [[0,1],[2,1],[1,1],[1,0],[2,0]] | ||
| <strong>输出:</strong> 1.00000 | ||
| <strong>解释:</strong> 最小面积的矩形出现在 [1,0],[1,1],[2,1],[2,0] 处,面积为 1。 | ||
| </pre> | ||
|
|
||
| #### 示例 3: | ||
|  | ||
| <pre> | ||
| <strong>输入:</strong> points = [[0,3],[1,2],[3,1],[1,3],[2,1]] | ||
| <strong>输出:</strong> 0 | ||
| <strong>解释:</strong> 没法从这些点中组成任何矩形。 | ||
| </pre> | ||
|
|
||
| #### 示例 4: | ||
| 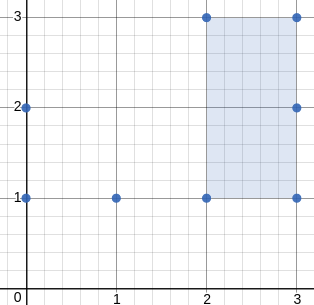 | ||
| <pre> | ||
| <strong>输入:</strong> [[3,1],[1,1],[0,1],[2,1],[3,3],[3,2],[0,2],[2,3]] | ||
| <strong>输出:</strong> 2.00000 | ||
| <strong>解释:</strong> 最小面积的矩形出现在 [2,1],[2,3],[3,3],[3,1] 处,面积为 2。 | ||
| </pre> | ||
|
|
||
| #### 提示: | ||
| 1. `1 <= points.length <= 50` | ||
| 2. `0 <= points[i][0] <= 40000` | ||
| 3. `0 <= points[i][1] <= 40000` | ||
| 4. 所有的点都是不同的。 | ||
| 5. 与真实值误差不超过 `10^-5` 的答案将视为正确结果。 | ||
|
|
||
| ## 题解 (Rust) | ||
|
|
||
| ### 1. 题解 | ||
| ```Rust | ||
| use std::collections::HashSet; | ||
|
|
||
| impl Solution { | ||
| pub fn min_area_free_rect(points: Vec<Vec<i32>>) -> f64 { | ||
| let points_set = points.iter().map(|p| (p[0], p[1])).collect::<HashSet<_>>(); | ||
| let mut ret = f64::NAN; | ||
|
|
||
| for i in 0..points.len() { | ||
| let (xi, yi) = (points[i][0], points[i][1]); | ||
|
|
||
| for j in i + 1..points.len() { | ||
| let (xj, yj) = (points[j][0], points[j][1]); | ||
| let ij2 = (xi - xj).pow(2) as f64 + (yi - yj).pow(2) as f64; | ||
|
|
||
| for k in j + 1..points.len() { | ||
| let (xk, yk) = (points[k][0], points[k][1]); | ||
| let ik2 = (xi - xk).pow(2) as f64 + (yi - yk).pow(2) as f64; | ||
| let jk2 = (xj - xk).pow(2) as f64 + (yj - yk).pow(2) as f64; | ||
|
|
||
| if ij2 + ik2 == jk2 && points_set.contains(&(xj + xk - xi, yj + yk - yi)) { | ||
| ret = ret.min(ij2.sqrt() * ik2.sqrt()); | ||
| } else if ij2 + jk2 == ik2 && points_set.contains(&(xi + xk - xj, yi + yk - yj)) | ||
| { | ||
| ret = ret.min(ij2.sqrt() * jk2.sqrt()); | ||
| } else if ik2 + jk2 == ij2 && points_set.contains(&(xi + xj - xk, yi + yj - yk)) | ||
| { | ||
| ret = ret.min(ik2.sqrt() * jk2.sqrt()); | ||
| } | ||
| } | ||
| } | ||
| } | ||
|
|
||
| if ret.is_nan() { | ||
| return 0.; | ||
| } | ||
|
|
||
| ret | ||
| } | ||
| } | ||
| ``` |
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
| Original file line number | Diff line number | Diff line change |
|---|---|---|
| @@ -0,0 +1,39 @@ | ||
| use std::collections::HashSet; | ||
|
|
||
| impl Solution { | ||
| pub fn min_area_free_rect(points: Vec<Vec<i32>>) -> f64 { | ||
| let points_set = points.iter().map(|p| (p[0], p[1])).collect::<HashSet<_>>(); | ||
| let mut ret = f64::NAN; | ||
|
|
||
| for i in 0..points.len() { | ||
| let (xi, yi) = (points[i][0], points[i][1]); | ||
|
|
||
| for j in i + 1..points.len() { | ||
| let (xj, yj) = (points[j][0], points[j][1]); | ||
| let ij2 = (xi - xj).pow(2) as f64 + (yi - yj).pow(2) as f64; | ||
|
|
||
| for k in j + 1..points.len() { | ||
| let (xk, yk) = (points[k][0], points[k][1]); | ||
| let ik2 = (xi - xk).pow(2) as f64 + (yi - yk).pow(2) as f64; | ||
| let jk2 = (xj - xk).pow(2) as f64 + (yj - yk).pow(2) as f64; | ||
|
|
||
| if ij2 + ik2 == jk2 && points_set.contains(&(xj + xk - xi, yj + yk - yi)) { | ||
| ret = ret.min(ij2.sqrt() * ik2.sqrt()); | ||
| } else if ij2 + jk2 == ik2 && points_set.contains(&(xi + xk - xj, yi + yk - yj)) | ||
| { | ||
| ret = ret.min(ij2.sqrt() * jk2.sqrt()); | ||
| } else if ik2 + jk2 == ij2 && points_set.contains(&(xi + xj - xk, yi + yj - yk)) | ||
| { | ||
| ret = ret.min(ik2.sqrt() * jk2.sqrt()); | ||
| } | ||
| } | ||
| } | ||
| } | ||
|
|
||
| if ret.is_nan() { | ||
| return 0.; | ||
| } | ||
|
|
||
| ret | ||
| } | ||
| } |
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters