You signed in with another tab or window. Reload to refresh your session.You signed out in another tab or window. Reload to refresh your session.You switched accounts on another tab or window. Reload to refresh your session.Dismiss alert
{{ message }}
This repository has been archived by the owner on Jan 28, 2021. It is now read-only.
Hello,
I do not know how to prove this lemma and I do not understand it either.
Let's suppose A = [2,5] and B = [1,6]
merge (A,B) = [1,2,5,6]
According to the lemma, Ci = minj(max(Aj, Bi-j)), so for all combinations of i and j, we want the one with the lowest j, right? minj means argmin j, doesn't it?
Then
C[0] = minj(max(A[0], B[0]) = 2 (note i = j = 0) but this is wrong! It should be 1, so should it be min instead of max?
C[1] = minj( {max(A[0], B[1-0]), max(A[1], B[0]) }) = minj( 6, 1) = 6 (because j = 0, in the other option j =1) but again this is wrong, it should be 2. If I use min instad of max, I would have minj(2, 1) = 2
Can someone explain to me what I am doing wrong and how to prove the lemma?
Thank you
The text was updated successfully, but these errors were encountered:
Hello,
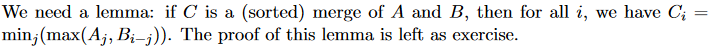
I do not know how to prove this lemma and I do not understand it either.
Let's suppose A = [2,5] and B = [1,6]
merge (A,B) = [1,2,5,6]
According to the lemma, Ci = minj(max(Aj, Bi-j)), so for all combinations of i and j, we want the one with the lowest j, right? minj means argmin j, doesn't it?
Then
C[0] = minj(max(A[0], B[0]) = 2 (note i = j = 0) but this is wrong! It should be 1, so should it be min instead of max?
C[1] = minj( {max(A[0], B[1-0]), max(A[1], B[0]) }) = minj( 6, 1) = 6 (because j = 0, in the other option j =1) but again this is wrong, it should be 2. If I use min instad of max, I would have minj(2, 1) = 2
Can someone explain to me what I am doing wrong and how to prove the lemma?
Thank you
The text was updated successfully, but these errors were encountered: