Note
You can download this example as a Python script: :jupyter-download:script:`orientation` or Jupyter Notebook: :jupyter-download📓`orientation`.
.. jupyter-execute:: import sympy as sm sm.init_printing(use_latex='mathjax')
In the study of multibody dynamics, we are interested in observing motion of connected and interacting objects in three dimensional space. This observation necessitates the concept of a frame of reference, or :term:`reference frame`, which is an abstraction defined by the set of all points in Euclidean space that is carried by the observer of any given state of motion. Practically speaking, it is useful to image your eye as an observer of motion. Your eye can orient itself in 3D space to view the motion of objects from any direction and the motion of objects will appear differently in the set of points associated with the reference frame attached to your eye depending on your eye's orientation.
It is important to note that a reference frame is not equivalent to a coordinate system. Any number of coordinate systems can be attached to a reference frame. We will characterize a reference frame by a right-handed set of mutually perpendicular unit vectors.
Vectors have a magnitude, direction, and sense (\pm). Unit vectors have a magnitude of 1. Unit vectors can be fixed, orientation-wise, to a reference frame. For a reference frame named N we will define the three mutually perpendicular unit vectors as \hat{n}_x, \hat{n}_y, \hat{n}_z where these right-handed cross products hold:
\hat{n}_x \times \hat{n}_y & = \hat{n}_z \\
\hat{n}_y \times \hat{n}_z & = \hat{n}_x \\
\hat{n}_z \times \hat{n}_x & = \hat{n}_y
Note
Unit vectors will be designated using the "hat", e.g. \hat{v}.
These unit vectors are fixed in the reference frame N. If a second reference frame A is defined, also with its set of right-handed mutually perpendicular unit vectors \hat{a}_x, \hat{a}_y, \hat{a}_z then we can establish the relative orientation of these two reference frames based on the angles among the two frames' unit vectors.
The image on the left and right represent the same set of right-handed mutually perpendicular unit vectors. Vectors, in general, do not have a position and can be drawn anywhere in the reference frame. Drawing them with their tails coincident is simply done for convenience.
Starting with two reference frames N and A in which their sets of unit vectors are initially aligned, the A frame can then be simply oriented about the common parallel z unit vectors of the two frames. We then say "reference frame A is oriented with respect to reference frame N about the shared z unit vectors through an angle \theta. A visual representation of this orientation is:
From the above figure these relationships between the \hat{a} and \hat{n} unit vectors can be deduced:
\hat{a}_x & = \cos{\theta} \hat{n}_x + \sin{\theta} \hat{n}_y + 0 \hat{n}_z \\
\hat{a}_y & = -\sin{\theta} \hat{n}_x + \cos{\theta} \hat{n}_y + 0 \hat{n}_z \\
\hat{a}_z & = 0 \hat{n}_x + 0 \hat{n}_y + 1 \hat{n}_z
These equations can also be written in matrix form:
\begin{bmatrix}
\hat{a}_x \\
\hat{a}_y \\
\hat{a}_z
\end{bmatrix}
=
\begin{bmatrix}
\cos{\theta} & \sin{\theta} & 0 \\
-\sin{\theta} & \cos{\theta} & 0 \\
0 & 0 & 1
\end{bmatrix}
\begin{bmatrix}
\hat{n}_x \\
\hat{n}_y \\
\hat{n}_z
\end{bmatrix}
This matrix uniquely describes the orientation between the two reference frames and so we can give it its own variable:
\begin{bmatrix}
\hat{a}_x \\
\hat{a}_y \\
\hat{a}_z
\end{bmatrix}
=
{}^A\mathbf{C}^N
\begin{bmatrix}
\hat{n}_x \\
\hat{n}_y \\
\hat{n}_z
\end{bmatrix}
This matrix {}^A\mathbf{C}^N maps vectors expressed in the N frame to vectors expressed in the A frame. This matrix has an important property, which we will demonstrate with SymPy. Start by creating the matrix:
.. jupyter-execute::
theta = sm.symbols('theta')
A_C_N = sm.Matrix([[sm.cos(theta), sm.sin(theta), 0],
[-sm.sin(theta), sm.cos(theta), 0],
[0, 0, 1]])
A_C_N
If we'd like the inverse relationship between the two sets of unit vectors and {}^A\mathbf{C}^N is invertible, then:
\begin{bmatrix}
\hat{n}_x \\
\hat{n}_y \\
\hat{n}_z
\end{bmatrix}
=
\left({}^A\mathbf{C}^N\right)^{-1}
\begin{bmatrix}
\hat{a}_x \\
\hat{a}_y \\
\hat{a}_z
\end{bmatrix}
SymPy can find this matrix inverse:
.. jupyter-execute:: sm.trigsimp(A_C_N.inv())
SymPy can also find the transpose of this matrix;
.. jupyter-execute:: A_C_N.transpose()
Notably, the inverse and the transpose are the same here. It turns out that this will be generally true for these matrices that describe the orientation between reference frames. Following the notation convention, this holds:
{}^N\mathbf{C}^A = \left({}^A\mathbf{C}^N\right)^{-1} = \left({}^A\mathbf{C}^N\right)^T
If now A is oriented relative to N and the pairwise angles between each \hat{a} and \hat{n} mutually perpendicular unit vectors are measured, an orientation matrix for an arbitrary orientation can be defined. For example, the figure below shows the three angles \alpha_{xx},\alpha_{xy},\alpha_{xz} relating \hat{a}_x to each \hat{n} unit vector.
Similarly to the simple example above, we can write these equations:
\hat{a}_x & = \cos\alpha_{xx} \hat{n}_x +\cos\alpha_{xy} \hat{n}_y + \cos\alpha_{xz} \hat{n}_z \\
\hat{a}_y & = \cos\alpha_{yx} \hat{n}_x +\cos\alpha_{yy} \hat{n}_y + \cos\alpha_{yz} \hat{n}_z \\
\hat{a}_z & = \cos\alpha_{zx} \hat{n}_x +\cos\alpha_{zy} \hat{n}_y + \cos\alpha_{zz} \hat{n}_z
Since we are working with mutually perpendicular unit vectors the cosine of the angle between each pair of unit vectors is equivalent to the dot product between the two vectors, so this also holds:
\hat{a}_x = (\hat{a}_x \cdot \hat{n}_x) \hat{n}_x + (\hat{a}_x \cdot \hat{n}_y) \hat{n}_y + (\hat{a}_x \cdot \hat{n}_z) \hat{n}_z \\
\hat{a}_y = (\hat{a}_y \cdot \hat{n}_x) \hat{n}_x + (\hat{a}_y \cdot \hat{n}_y) \hat{n}_y + (\hat{a}_y \cdot \hat{n}_z) \hat{n}_z \\
\hat{a}_x = (\hat{a}_z \cdot \hat{n}_x) \hat{n}_x + (\hat{a}_z \cdot \hat{n}_y) \hat{n}_y + (\hat{a}_z \cdot \hat{n}_z) \hat{n}_z \\
Now the general :term:`direction cosine matrix` of A with respect to N is defined as:
\begin{bmatrix}
\hat{a}_x \\
\hat{a}_y \\
\hat{a}_z
\end{bmatrix}
=
\begin{bmatrix}
\hat{a}_x \cdot \hat{n}_x &\hat{a}_x \cdot \hat{n}_y & \hat{a}_x \cdot \hat{n}_z \\
\hat{a}_y \cdot \hat{n}_x &\hat{a}_y \cdot \hat{n}_y & \hat{a}_y \cdot \hat{n}_z \\
\hat{a}_z \cdot \hat{n}_x &\hat{a}_z \cdot \hat{n}_y & \hat{a}_z \cdot \hat{n}_z
\end{bmatrix}
\begin{bmatrix}
\hat{n}_x \\
\hat{n}_y \\
\hat{n}_z
\end{bmatrix}
where the general direction cosine matrix is then:
{}^A\mathbf{C}^N
=
\begin{bmatrix}
\hat{a}_x \cdot \hat{n}_x &\hat{a}_x \cdot \hat{n}_y & \hat{a}_x \cdot \hat{n}_z \\
\hat{a}_y \cdot \hat{n}_x &\hat{a}_y \cdot \hat{n}_y & \hat{a}_y \cdot \hat{n}_z \\
\hat{a}_z \cdot \hat{n}_x &\hat{a}_z \cdot \hat{n}_y & \hat{a}_z \cdot \hat{n}_z
\end{bmatrix}
This matrix uniquely defines the relative orientation between reference frames N and A, it is invertible, and its inverse is equal to the transpose, as shown above in the simple example. The direction cosine matrix found in the prior section for a simple orientation is a specific case of this more general definition. The direction cosine matrix is also referred to as a rotation matrix in some texts.
Successive orientations of a series of reference frames provides a convenient way to manage orientation among more than a single pair. Below, an additional reference frame B is shown that is simply oriented with respect to A in the same way that A is from N above.
We know that we can define these two relationships between each pair of reference frames:
\begin{bmatrix}
\hat{a}_x \\
\hat{a}_y \\
\hat{a}_z
\end{bmatrix}
=
{}^A\mathbf{C}^N
\begin{bmatrix}
\hat{n}_x \\
\hat{n}_y \\
\hat{n}_z
\end{bmatrix}
\begin{bmatrix}
\hat{b}_x \\
\hat{b}_y \\
\hat{b}_z
\end{bmatrix}
=
{}^B\mathbf{C}^A
\begin{bmatrix}
\hat{a}_x \\
\hat{a}_y \\
\hat{a}_z
\end{bmatrix}
Now, substitute the first equation into the second to get:
\begin{bmatrix}
\hat{b}_x \\
\hat{b}_y \\
\hat{b}_z
\end{bmatrix}
=
{}^B\mathbf{C}^A
{}^A\mathbf{C}^N
\begin{bmatrix}
\hat{n}_x \\
\hat{n}_y \\
\hat{n}_z
\end{bmatrix}
showing that the direction cosine matrix between B and N results from matrix multiplying the intermediate direction cosine matrices.
{}^B\mathbf{C}^N
=
{}^B\mathbf{C}^A
{}^A\mathbf{C}^N
This holds for any series of successive orientations:
{}^Z\mathbf{C}^A
=
{}^Z\mathbf{C}^Y
{}^Y\mathbf{C}^X
\ldots
{}^C\mathbf{C}^B
{}^B\mathbf{C}^A
Using :numref:`orientation-simple-successive` as an explicit example of this property, we start with the already defined {}^A\mathbf{C}^N:
.. jupyter-execute:: A_C_N
{}^B\mathbf{C}^A can then be defined similarly:
.. jupyter-execute::
alpha = sm.symbols('alpha')
B_C_A = sm.Matrix([[sm.cos(alpha), sm.sin(alpha), 0],
[-sm.sin(alpha), sm.cos(alpha), 0],
[0, 0, 1]])
B_C_A
Finally, {}^B\mathbf{C}^N can be found by matrix multiplication:
.. jupyter-execute:: B_C_N = B_C_A*A_C_N B_C_N
Simplifying these trigonometric expressions shows the expected result:
.. jupyter-execute:: sm.trigsimp(B_C_N)
As shown above, SymPy nicely handles the formulation of direction cosine matrices, but SymPy offers a more useful abstraction for these things. The :external:py:mod:`sympy.physics.mechanics` module includes numerous objects and functions that ease the bookkeeping and mental models needed to manage various aspects of multibody dynamics. We will import the module consistently as:
.. jupyter-execute:: import sympy.physics.mechanics as me
mechanics includes a way to define and orient reference frames. To create a
reference frame, use :external:py:class:`ReferenceFrame()
<sympy.physics.vector.frame.ReferenceFrame>` and provide a name for your frame.
.. jupyter-execute::
N = me.ReferenceFrame('N')
The right-handed mutually perpendicular unit vectors associated with a
reference frame are accessed with .x, .y, and .z, like so:
.. jupyter-execute:: N.x, N.y, N.z
Using :numref:`orientation-simple-successive` again as an example, we can define all three reference frames:
.. jupyter-execute::
A = me.ReferenceFrame('A')
B = me.ReferenceFrame('B')
N, A, B
We have already defined the direction cosine matrices for these two successive orientations. For example:
.. jupyter-execute:: A_C_N
relates A and N. ReferenceFrame objects can be oriented wrt
respect to one another. The :external:py:meth:`orient_explicit()
<sympy.physics.vector.frame.ReferenceFrame.orient_explicit>` method allows you
to set the direction cosine matrix explicitly:
.. jupyter-execute:: N.orient_explicit(A, A_C_N)
Now you can ask for the direction cosine matrix of A with respect to N, i.e. {}^A\mathbf{C}^N, using the :external:py:meth:`dcm() <sympy.physics.vector.frame.ReferenceFrame.orient_explicit>` method:
.. jupyter-execute:: A.dcm(N)
Warning
Note very carefully what version of the direction cosine matrix you pass to
.orient_explicit(). Check its docstring with N.orient_explicit?.
But even better for this case is the :external:py:meth:`orient_axis() <sympy.physics.vector.frame.ReferenceFrame.orient_axis>` method. This method allows you to define simple orientations between reference frames more naturally. You provide the frame to orient from, the angle to orient through, and the vector to orient about. For example, orient B with respect to A through \alpha about \hat{a}_z by:
.. jupyter-execute:: B.orient_axis(A, alpha, A.z)
Now the direction cosine matrix is automatically calculated and is returned
with the .dcm() method:
.. jupyter-execute:: B.dcm(A)
The inverse is also defined on A:
.. jupyter-execute:: A.dcm(B)
So each pair of reference frames are aware of its orientation partner (or partners). Now that we've established orientations between N and A and A and B, we might want to know the relationships between B and N. Remember that matrix multiplication of the two successive direction cosine matrices provides the answer:
.. jupyter-execute:: sm.trigsimp(B.dcm(A)*A.dcm(N))
But, the answer can also be found by calling .dcm() with the two reference
frames in question. As long as there is a successive path between the two
reference frames, this is sufficient for obtaining the desired direction cosine
matrix:
.. jupyter-execute:: sm.trigsimp(B.dcm(N))
Lastly, recall the general definition of the direction cosine matrix. We showed
that the dot product of pairs of unit vectors give the entries to the direction
cosine matrix. mechanics has a :external:py:func:`dot()
<sympy.physics.vector.functions.dot>` function that can calculate the dot
product of two vectors. Using it on two of the unit vector pairs returns the
expected direction cosine matrix entry:
.. jupyter-execute:: sm.trigsimp(me.dot(B.x, N.x))
This camera stabilization gimbal has three revolute joints that orient the camera D relative to the handgrip frame A.

Four reference frames labeled on the Turnigy Pro Steady Hand Camera Gimbal. Image copyright HobbyKing, used under fair use for educational purposes.
If we introduce two additional auxiliary reference frames: B and C, we can use three successive simple orientations to go from A to D. Using the same technique for the successive simple orientations above, but now managing the three dimensional orientations, we can formulate the direction cosine matrices for the reference frames.
Watch this video to get a sense of the orientation axes for each intermediate auxiliary reference frame:
We first orient B with respect to A about the shared z unit vector through the angle \psi, as shown below:
View of the A and B x\textrm{-}y plane showing the orientation of B relative to A about z through angle \psi.
and then using ReferenceFrame objects:
.. jupyter-execute::
psi = sm.symbols('psi')
A = me.ReferenceFrame('A')
B = me.ReferenceFrame('B')
B.orient_axis(A, psi, A.z)
B.dcm(A)
Now orient C with respect to B about their shared x unit vector through angle \theta.
View of the B and C y\textrm{-}z plane showing the orientation of C relative to B about x through angle \theta.
.. jupyter-execute::
theta = sm.symbols('theta')
C = me.ReferenceFrame('C')
C.orient_axis(B, theta, B.x)
C.dcm(B)
Finally, orient the camera D with respect to C about their shared y unit vector through the angle \phi.
View of the C and D x\textrm{-}z plane showing the orientation of D relative to C about y through angle \varphi.
.. jupyter-execute::
phi = sm.symbols('varphi')
D = me.ReferenceFrame('D')
D.orient_axis(C, phi, C.y)
D.dcm(C)
With all of the intermediate orientations defined, when can now ask for the relationship {}^D\mathbf{C}^A of the camera D relative to the handgrip frame A:
.. jupyter-execute:: D.dcm(A)
With these three orientations the camera can be oriented arbitrarily relative to the handgrip frame. These successive z\textrm{-}x\textrm{-}y orientations are a standard way of describing the orientation of two reference frames and are often referred to as Euler Angles [*].
There are 12 valid sets of successive orientations. We will also refer to these 12 possible orientation sets as body fixed orientations. As we will soon see, a rigid body and a reference frame are synonymous from an orientation perspective and each successive orientations rotates about a shared unit vector fixed in both of the reference frames (or bodies), thus "body fixed orientations". The method :external:py:meth:`orient_body_fixed() <sympy.physics.vector.frame.ReferenceFrame.orient_body_fixed>` can be used to establish the relationship between A and D without the need to create auxiliary reference frames B and C:
.. jupyter-execute::
A = me.ReferenceFrame('A')
D = me.ReferenceFrame('D')
D.orient_body_fixed(A, (psi, theta, phi), 'zxy')
D.dcm(A)
Euler technically only discovered 6 of the 12 orientation sets. One of these sets is shown in this figure:
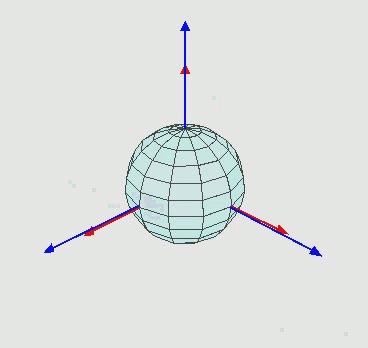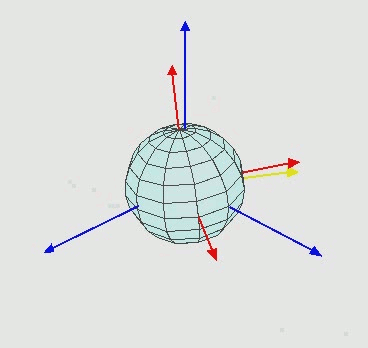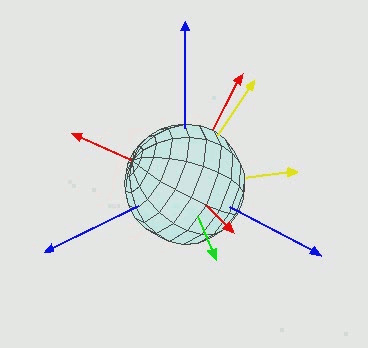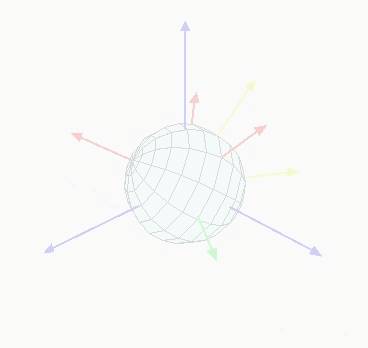
z\textrm{-}x\textrm{-}z Euler angle visualization.
The z\textrm{-}x\textrm{-}z Euler angles shown in :numref:`orientation-euler-animation` are then created like so:
.. jupyter-execute::
A = me.ReferenceFrame('A')
D = me.ReferenceFrame('D')
D.orient_body_fixed(A, (psi, theta, phi), 'zxz')
D.dcm(A)
Footnotes
| [*] | Technically, this set of angles for the gimbal are one of the 6 Tait-Bryan angles, but "Euler Angles" is used as a general term to describe both Tait-Bryan angles and "proper Euler angles". |