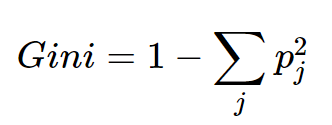- Problem Description (Brief Write Up)
- Exploratory Data Analysis (EDA)
- Data Pre-processing
- Model Selection
- Evaluation
- Discussion and Possible Improvements
The data set we will be working on contains payment information of 30,000 credit card holders obtained from a bank in Taiwan.
Each data sample is described by 23 feature attributes and a binary target feature (default or not) valued 0 (= not default) or 1 (= default).
The 23 explanatory attributes are:
X1: Amount of the given credit (NT dollar): it includes both the individual consumer credit and his/her family (supplementary) credit.
X2: Gender (1 = male; 2 = female).
X3: Education (1 = graduate school; 2 = university; 3 = high school; 4 = others).
X4: Marital status (1 = married; 2 = single; 3 = others).
X5: Age (year).
The measurement scale for the repayment status is: -1 = pay duly; 1 = payment delay for one month; 2 = payment delay for two months, . . . 8 = payment delay for eight months; 9 = payment delay for nine months and above.
X6 = the repayment status in September, 2005
X7 = the repayment status in August, 2005
X8 = the repayment status in July, 2005
X9 = the repayment status in June, 2005
X10 = the repayment status in May, 2005
X11 = the repayment status in April, 2005.
X12 = amount of bill statement in September, 2005;
X13 = amount of bill statement in August, 2005
. . .
X17 = amount of bill statement in April, 2005.
X18 = amount paid in September, 2005
X19 = amount paid in August, 2005
. . .
X23 = amount paid in April, 2005.
In this section we will explore the data set, its shape and its features to get an idea of the data.
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
url = 'https://raw.githubusercontent.com/reonho/bt2101disrudy/master/card.csv'
df = pd.read_csv(url, header = 1, index_col = 0)
# Dataset is now stored in a Pandas Dataframe
df0 = df
#rename the target variable to "Y" for convenience
df["Y"] = df["default payment next month"]
df = df.drop("default payment next month", axis = 1)
df.head()
.dataframe tbody tr th {
vertical-align: top;
}
.dataframe thead th {
text-align: right;
}
| LIMIT_BAL | SEX | EDUCATION | MARRIAGE | AGE | PAY_0 | PAY_2 | PAY_3 | PAY_4 | PAY_5 | ... | BILL_AMT4 | BILL_AMT5 | BILL_AMT6 | PAY_AMT1 | PAY_AMT2 | PAY_AMT3 | PAY_AMT4 | PAY_AMT5 | PAY_AMT6 | Y | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ID | |||||||||||||||||||||
| 1 | 20000 | 2 | 2 | 1 | 24 | 2 | 2 | -1 | -1 | -2 | ... | 0 | 0 | 0 | 0 | 689 | 0 | 0 | 0 | 0 | 1 |
| 2 | 120000 | 2 | 2 | 2 | 26 | -1 | 2 | 0 | 0 | 0 | ... | 3272 | 3455 | 3261 | 0 | 1000 | 1000 | 1000 | 0 | 2000 | 1 |
| 3 | 90000 | 2 | 2 | 2 | 34 | 0 | 0 | 0 | 0 | 0 | ... | 14331 | 14948 | 15549 | 1518 | 1500 | 1000 | 1000 | 1000 | 5000 | 0 |
| 4 | 50000 | 2 | 2 | 1 | 37 | 0 | 0 | 0 | 0 | 0 | ... | 28314 | 28959 | 29547 | 2000 | 2019 | 1200 | 1100 | 1069 | 1000 | 0 |
| 5 | 50000 | 1 | 2 | 1 | 57 | -1 | 0 | -1 | 0 | 0 | ... | 20940 | 19146 | 19131 | 2000 | 36681 | 10000 | 9000 | 689 | 679 | 0 |
5 rows × 24 columns
size = df.shape
print("Data has {} Columns and {} Rows".format(size[1], size[0]))
Data has 24 Columns and 30000 Rows
#check for null values
df.isnull().any().sum()
0
There are no null values in the data.
We can also calculate some summary statistics for each attribute.
df.describe()
.dataframe tbody tr th {
vertical-align: top;
}
.dataframe thead th {
text-align: right;
}
| LIMIT_BAL | SEX | EDUCATION | MARRIAGE | AGE | PAY_0 | PAY_2 | PAY_3 | PAY_4 | PAY_5 | ... | BILL_AMT4 | BILL_AMT5 | BILL_AMT6 | PAY_AMT1 | PAY_AMT2 | PAY_AMT3 | PAY_AMT4 | PAY_AMT5 | PAY_AMT6 | Y | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| count | 30000.000000 | 30000.000000 | 30000.000000 | 30000.000000 | 30000.000000 | 30000.000000 | 30000.000000 | 30000.000000 | 30000.000000 | 30000.000000 | ... | 30000.000000 | 30000.000000 | 30000.000000 | 30000.000000 | 3.000000e+04 | 30000.00000 | 30000.000000 | 30000.000000 | 30000.000000 | 30000.000000 |
| mean | 167484.322667 | 1.603733 | 1.853133 | 1.551867 | 35.485500 | -0.016700 | -0.133767 | -0.166200 | -0.220667 | -0.266200 | ... | 43262.948967 | 40311.400967 | 38871.760400 | 5663.580500 | 5.921163e+03 | 5225.68150 | 4826.076867 | 4799.387633 | 5215.502567 | 0.221200 |
| std | 129747.661567 | 0.489129 | 0.790349 | 0.521970 | 9.217904 | 1.123802 | 1.197186 | 1.196868 | 1.169139 | 1.133187 | ... | 64332.856134 | 60797.155770 | 59554.107537 | 16563.280354 | 2.304087e+04 | 17606.96147 | 15666.159744 | 15278.305679 | 17777.465775 | 0.415062 |
| min | 10000.000000 | 1.000000 | 0.000000 | 0.000000 | 21.000000 | -2.000000 | -2.000000 | -2.000000 | -2.000000 | -2.000000 | ... | -170000.000000 | -81334.000000 | -339603.000000 | 0.000000 | 0.000000e+00 | 0.00000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 |
| 25% | 50000.000000 | 1.000000 | 1.000000 | 1.000000 | 28.000000 | -1.000000 | -1.000000 | -1.000000 | -1.000000 | -1.000000 | ... | 2326.750000 | 1763.000000 | 1256.000000 | 1000.000000 | 8.330000e+02 | 390.00000 | 296.000000 | 252.500000 | 117.750000 | 0.000000 |
| 50% | 140000.000000 | 2.000000 | 2.000000 | 2.000000 | 34.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | ... | 19052.000000 | 18104.500000 | 17071.000000 | 2100.000000 | 2.009000e+03 | 1800.00000 | 1500.000000 | 1500.000000 | 1500.000000 | 0.000000 |
| 75% | 240000.000000 | 2.000000 | 2.000000 | 2.000000 | 41.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | ... | 54506.000000 | 50190.500000 | 49198.250000 | 5006.000000 | 5.000000e+03 | 4505.00000 | 4013.250000 | 4031.500000 | 4000.000000 | 0.000000 |
| max | 1000000.000000 | 2.000000 | 6.000000 | 3.000000 | 79.000000 | 8.000000 | 8.000000 | 8.000000 | 8.000000 | 8.000000 | ... | 891586.000000 | 927171.000000 | 961664.000000 | 873552.000000 | 1.684259e+06 | 896040.00000 | 621000.000000 | 426529.000000 | 528666.000000 | 1.000000 |
8 rows × 24 columns
1) Exploring target attribute:
All = df.shape[0]
default = df[df['Y'] == 1]
nondefault = df[df['Y'] == 0]
x = len(default)/All
y = len(nondefault)/All
print('defaults :',x*100,'%')
print('non defaults :',y*100,'%')
defaults : 22.12 %
non defaults : 77.88000000000001 %
# plotting target attribute against frequency
labels = ['non default','default']
classes = pd.value_counts(df['Y'], sort = True)
classes.plot(kind = 'bar', rot=0)
plt.title("Target attribute distribution")
plt.xticks(range(2), labels)
plt.xlabel("Class")
plt.ylabel("Frequency")
Text(0, 0.5, 'Frequency')
2) Exploring categorical attributes
Categorical attributes are:
- Sex
- Education
- Marriage
2a) Checking formatting for categorical attributes:
Since all categorical attributes are in numerical format, there is no need to convert them into numerical factors.
2b) Analysis of categorical data groups
- Sex
- Education
- Marriage
print(df["SEX"].value_counts().apply(lambda r: r/All*100))
print("--------------------------------------------------------")
print(df["EDUCATION"].value_counts().apply(lambda r: r/All*100))
print("--------------------------------------------------------")
print(df["MARRIAGE"].value_counts().apply(lambda r: r/All*100))
2 60.373333
1 39.626667
Name: SEX, dtype: float64
--------------------------------------------------------
2 46.766667
1 35.283333
3 16.390000
5 0.933333
4 0.410000
6 0.170000
0 0.046667
Name: EDUCATION, dtype: float64
--------------------------------------------------------
2 53.213333
1 45.530000
3 1.076667
0 0.180000
Name: MARRIAGE, dtype: float64
Conclusion
- Categorical variable SEX does not seem to have any missing/extra groups, and it is separated into Male = 1 and Female = 2
- Categorical variable MARRIAGE seems to have unknown group = 0, which could be assumed to be missing data, with other groups being Married = 1, Single = 2, Others = 3
- Categorical variable EDUCATION seems to have unknown group = 0,5,6, with other groups being graduate school = 1, university = 2, high school = 3, others = 4
2c) Analysing the relationship between categorical attributes and default paymment (target attribute)
- Sex
- Education
- Marriage
#proportion of target attribute (for reference)
print('Total target attributes:')
print('non defaults :',y*100,'%')
print('defaults :',x*100,'%')
print("--------------------------------------------------------")
#analysing default payment with Sex
sex_target = pd.crosstab(df["Y"], df["SEX"]).apply(lambda r: r/r.sum()*100).rename(columns = {1: "Male", 2: "Female"}, index = {0: "non defaults", 1: "defaults"})
print(sex_target)
print("--------------------------------------------------------")
#analysing default payment with education
education_target = pd.crosstab(df["Y"], df["EDUCATION"]).apply(lambda r: r/r.sum()*100).rename(index = {0: "non defaults", 1: "defaults"})
print(education_target)
print("--------------------------------------------------------")
#analysing default payment with marriage
marriage_target = pd.crosstab(df["Y"], df["MARRIAGE"]).apply(lambda r: r/r.sum()*100).rename(columns = {0: "unknown",1: "married", 2: "single", 3: "others"},index = {0: "non defaults", 1: "defaults"})
print(marriage_target)
Total target attributes:
non defaults : 77.88000000000001 %
defaults : 22.12 %
--------------------------------------------------------
SEX Male Female
Y
non defaults 75.832773 79.223719
defaults 24.167227 20.776281
--------------------------------------------------------
EDUCATION 0 1 2 3 4 5 \
Y
non defaults 100.0 80.765234 76.265146 74.842384 94.308943 93.571429
defaults 0.0 19.234766 23.734854 25.157616 5.691057 6.428571
EDUCATION 6
Y
non defaults 84.313725
defaults 15.686275
--------------------------------------------------------
MARRIAGE unknown married single others
Y
non defaults 90.740741 76.528296 79.071661 73.993808
defaults 9.259259 23.471704 20.928339 26.006192
# we would like to conduct a chi square test of independence using the contingency tables above
import scipy.stats as sp_stat
def sigf(p, confidence):
return str(p) + " *** [Significant at the " + str(int(confidence*100)) + "% Level]" if p < 1-confidence else p
#print the p values for the test statistic of each chi-sq test
print("SEX:", sigf(sp_stat.chi2_contingency(sex_target)[1], 0.95))
print("EDUCATION:", sigf(sp_stat.chi2_contingency(education_target)[1],0.95))
print("MARRIAGE:", sigf(sp_stat.chi2_contingency(marriage_target)[1],0.95))
SEX: 0.6854422910010494
EDUCATION: 1.0276815835411287e-08 *** [Significant at the 95% Level]
MARRIAGE: 0.016161318279331434 *** [Significant at the 95% Level]
Conclusion
Categorical attributes EDUCATION and MARRIAGE are associated with the target variable.
We will omit SEX from our models as it is statistically insignificant.
Categorical attributes SEX and MARRIAGE have approximately uniform distributions throughout groups of categories.
3) Analysis of Numerical Attributes
The numerical attributes are:
#printing numerical attributes
pd.DataFrame(df.drop(['SEX', 'EDUCATION', 'MARRIAGE','Y'], axis = 1).columns)
.dataframe tbody tr th {
vertical-align: top;
}
.dataframe thead th {
text-align: right;
}
| 0 | |
|---|---|
| 0 | LIMIT_BAL |
| 1 | AGE |
| 2 | PAY_0 |
| 3 | PAY_2 |
| 4 | PAY_3 |
| 5 | PAY_4 |
| 6 | PAY_5 |
| 7 | PAY_6 |
| 8 | BILL_AMT1 |
| 9 | BILL_AMT2 |
| 10 | BILL_AMT3 |
| 11 | BILL_AMT4 |
| 12 | BILL_AMT5 |
| 13 | BILL_AMT6 |
| 14 | PAY_AMT1 |
| 15 | PAY_AMT2 |
| 16 | PAY_AMT3 |
| 17 | PAY_AMT4 |
| 18 | PAY_AMT5 |
| 19 | PAY_AMT6 |
Meaning of attributes PAY_0 to PAY_6
The numeric value in these attributes shows the past history of a credit card holder, example -2 means: No consumption of credit card, -1 means that holder paid the full balance, 0 means the use of revolving credit; 1= paymentdelay of one month; 2= payment delay of two months and so on.
3a) Limit Balance
#Find out min and max value of LIMIT BALANCE
print(df["LIMIT_BAL"].describe())
count 30000.000000
mean 167484.322667
std 129747.661567
min 10000.000000
25% 50000.000000
50% 140000.000000
75% 240000.000000
max 1000000.000000
Name: LIMIT_BAL, dtype: float64
sns.distplot(df["LIMIT_BAL"]).set_title('Distribution of Limit Balance')
Text(0.5, 1.0, 'Distribution of Limit Balance')
3b) Analysis of Age
sns.distplot(df.AGE)
<matplotlib.axes._subplots.AxesSubplot at 0x25606f88748>
To find out the relationships between the features, we calculate the absolute value of R with the target for all attributes. (R = Correlation Coefficient)
#absolute correlation coefficient
pd.DataFrame(df.drop(['SEX', 'EDUCATION', 'MARRIAGE','Y'], axis=1).apply(lambda x: x.corr(df.Y) if x.corr(df.Y) > 0 else -x.corr(df.Y)).sort_values(ascending = False))
.dataframe tbody tr th {
vertical-align: top;
}
.dataframe thead th {
text-align: right;
}
| 0 | |
|---|---|
| PAY_0 | 0.324794 |
| PAY_2 | 0.263551 |
| PAY_3 | 0.235253 |
| PAY_4 | 0.216614 |
| PAY_5 | 0.204149 |
| PAY_6 | 0.186866 |
| LIMIT_BAL | 0.153520 |
| PAY_AMT1 | 0.072929 |
| PAY_AMT2 | 0.058579 |
| PAY_AMT4 | 0.056827 |
| PAY_AMT3 | 0.056250 |
| PAY_AMT5 | 0.055124 |
| PAY_AMT6 | 0.053183 |
| BILL_AMT1 | 0.019644 |
| BILL_AMT2 | 0.014193 |
| BILL_AMT3 | 0.014076 |
| AGE | 0.013890 |
| BILL_AMT4 | 0.010156 |
| BILL_AMT5 | 0.006760 |
| BILL_AMT6 | 0.005372 |
We observe that the "repayment status" attributes are the most highly correlated with the target variable and we would expect them to be more significant in predicting credit default. In fact the later the status, the more correlated it is.
The least correlated attributes are the bill amounts.
We can also generate a correlation matrix (heatmap) to see which features are the most correlated with each other.
f = plt.figure(figsize=(19, 15))
plt.matshow(df.corr(), fignum=f.number)
plt.xticks(range(df.shape[1]), df.columns, fontsize=14, rotation=45)
plt.yticks(range(df.shape[1]), df.columns, fontsize=14)
cb = plt.colorbar()
cb.ax.tick_params(labelsize=14)
plt.title('Correlation Matrix', fontsize=16)
Text(0.5, 1.05, 'Correlation Matrix')
The heatmap reveals that the payment and billed amounts across the 5 months are highly correlated with each other. Highly Correlated factors should be removed before carrying out any regression to prevent multicollinearity.
- Linear regression
- Scatterplot matrix
- Boxplot matrix
???
- get rid of unknown attributes
- normalise
- pca?
In this part, we will fit machine learning models learnt in BT2101 to this classification problem, and pick the model that can produce the best results.
We will be attempting to fit the following models:
- K-Nearest Neighbour
- Support Vector Machine
- Decision Tree
- Naive Bayes Classifier
- Logistic Regression
- Neural Network
#using kfold to create train test splits
import sklearn.model_selection as skm
kf = skm.KFold(10)
#using holdout sampling for train test split
ft = df.drop("Y", axis = 1)
target = df["Y"]
X_train,X_test,y_train,y_test = skm.train_test_split(ft,target,test_size=0.20)
To make things easier, we define a get_roc function that will plot an ROC curve for all the models we evaluate
def get_roc(model, y_test, x_test, name):
fpr = roc_curve(y_test,model.predict_proba(X_test)[:,1])[0]
tpr = roc_curve(y_test,model.predict_proba(X_test)[:,1])[1]
plt.plot([0, 1], [0, 1], color='navy', linestyle='--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Receiver operating characteristic for ' + name)
plt.plot(fpr,tpr,label='ROC curve (AUC = %0.2f)' % (auc(fpr, tpr)))
plt.legend(loc="lower right")
plt.show()
def confusion(model, y_test, X_test, name):
conf = pd.crosstab(y_test,model.predict(X_test), rownames=['Actual'], colnames=['Predicted'])
print("Of " + str(conf[0][1] + conf[1][1]) + " Defaulters, the " + name + " identified " + str(conf[1][1]))
return conf
We will select the model based on the model evaluation. The key metrics we will compute are: (Need someone to fill in the formula)
- Accuracy
- Precision
- Recall
- F1 Measure
- AUROC
Because of the nature of a default detection problem, we would like to prioritise recall for defaults. This means we will place more importance in correctly identifying a defaulter than avoiding misclassifying a non-defaulter. (Assumming that the bank loses more money when lending to a defaulter than not lending to a non-defaulter)
This part aims to provide a benchmark accuracy for our models, i.e. a random classifier with (expected) accuracy of 0.5.
from random import *
import sklearn.metrics as skmt
def rnjezus(i):
return randint(0, 1)
# Holdout sampling
print("Holdout Sample Accuracy:")
print(skmt.classification_report(y_test, list(map(lambda x : rnjezus(x), range(len(X_test))))))
# K-fold
accuracies = []
for train,test in kf.split(df):
prediction = list(map(lambda x : rnjezus(x), test))
actual = list(df["Y"][test+1])
#By definition the columns correspond to the predicted values and rows are the actuals
conf_mat = skmt.confusion_matrix(actual, prediction)
#print(pd.DataFrame(conf_mat))
accuracies.append(skmt.accuracy_score(actual, prediction))
print("Kfold Average Accuracy:", sum(accuracies)/len(accuracies))
Holdout Sample Accuracy:
precision recall f1-score support
0 0.78 0.50 0.61 4673
1 0.22 0.51 0.31 1327
accuracy 0.50 6000
macro avg 0.50 0.51 0.46 6000
weighted avg 0.66 0.50 0.54 6000
Kfold Average Accuracy: 0.4919999999999999
import numpy as np
from sklearn.neighbors import KNeighborsClassifier
neighbours = np.arange(1,25)
train_accuracy =np.empty(len(neighbours))
test_accuracy = np.empty(len(neighbours))
for i,k in enumerate(neighbours):
#Setup a knn classifier with k neighbors
knn=KNeighborsClassifier(n_neighbors=k,algorithm="kd_tree",n_jobs=-1)
#Fit the model
knn.fit(X_train,y_train.ravel())
#Compute accuracy on the training set
train_accuracy[i] = knn.score(X_train, y_train.ravel())
#Compute accuracy on the test set
test_accuracy[i] = knn.score(X_test, y_test.ravel())
#Generate plot
plt.title('k-NN Varying number of neighbors')
plt.plot(neighbours, test_accuracy, label='Testing Accuracy')
plt.plot(neighbours, train_accuracy, label='Training accuracy')
plt.legend()
plt.xlabel('Number of neighbors')
plt.ylabel('Accuracy')
plt.show()
# best k:
idx = np.where(test_accuracy == max(test_accuracy))
k = neighbours[idx][0]
knn = KNeighborsClassifier(n_neighbors=k,algorithm="kd_tree",n_jobs=-1)
knn.fit(X_train,y_train.ravel())
print(skmt.classification_report(y_test,knn.predict(X_test)))
precision recall f1-score support
0 0.79 0.98 0.87 4673
1 0.51 0.08 0.13 1327
accuracy 0.78 6000
macro avg 0.65 0.53 0.50 6000
weighted avg 0.73 0.78 0.71 6000
Despite a reasonably high accuracy, the KNN model has very low recall for defaults.
confusion(knn, y_test, X_test, "KNN")
Of 1327 Defaulters, the KNN identified 101
.dataframe tbody tr th {
vertical-align: top;
}
.dataframe thead th {
text-align: right;
}
| Predicted | 0 | 1 |
|---|---|---|
| Actual | ||
| 0 | 4576 | 97 |
| 1 | 1226 | 101 |
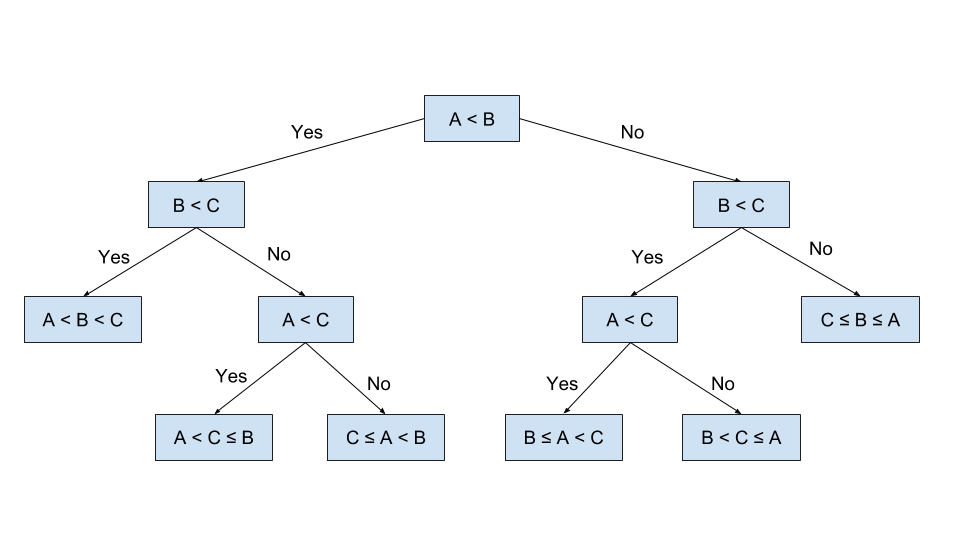
The decision tree algorithm aims to recursively split the data points in the training set until the data points are completely separated or well separated. At each iteration, the tree splits the datasets by the feature(s) that give the maximum reduction in heterogeneity, which is calculated by a heterogeneity index.
Below is a binary decision tree that has been split for a few iterations.
Since the target for this project is binary (fraud = yes or no) we will be building a binary decision tree, using the the GINI Index as the Heterogeneity index. The GINI is given by:
The GINI index measures how heterogenous a single node is (0 being completely homogenous and 1 being heterogenous). For each possible split, we will calculate the weighted sum of the GINI indices of the child nodes, and choose the split that results in the maximum information gain. i.e. reduction in the weighted sum of the GINI Index.
We will now construct a simple decision tree using the GINI index.
from sklearn.tree import DecisionTreeClassifier
from sklearn.metrics import *
tree = DecisionTreeClassifier()
tree.fit(X_train, y_train)
DecisionTreeClassifier(class_weight=None, criterion='gini', max_depth=None,
max_features=None, max_leaf_nodes=None,
min_impurity_decrease=0.0, min_impurity_split=None,
min_samples_leaf=1, min_samples_split=2,
min_weight_fraction_leaf=0.0, presort=False,
random_state=None, splitter='best')
print(classification_report(y_train, tree.predict(X_train)))
precision recall f1-score support
0 1.00 1.00 1.00 18691
1 1.00 1.00 1.00 5309
accuracy 1.00 24000
macro avg 1.00 1.00 1.00 24000
weighted avg 1.00 1.00 1.00 24000
The training set accuracy is 1, which means the datapoints are completely separated by the decision tree. We evaluate on the test set below.
confusion(tree, y_test, X_test, "Decision Tree (GINI)")
Of 1327 Defaulters, the Decision Tree (GINI) identified 550
.dataframe tbody tr th {
vertical-align: top;
}
.dataframe thead th {
text-align: right;
}
| Predicted | 0 | 1 |
|---|---|---|
| Actual | ||
| 0 | 3804 | 869 |
| 1 | 777 | 550 |
get_roc(tree, y_test, X_test, "Decision Tree (GINI)")
print(classification_report(y_test, tree.predict(X_test)))
precision recall f1-score support
0 0.83 0.81 0.82 4673
1 0.39 0.41 0.40 1327
accuracy 0.73 6000
macro avg 0.61 0.61 0.61 6000
weighted avg 0.73 0.73 0.73 6000
Random Forest is an ensemble method for the decision tree algorithm. It works by randomly choosing different features and data points to train multiple trees (that is, to form a forest) - and the resulting prediction is decided by the votes from all the trees.
Decision Trees are prone to overfitting on the training data, which reduces the performance on the test set. Random Forest mitigates this by training multiple trees. Random Forest is a form of bagging ensemble where the trees are trained concurrently.
To keep things consistent, our Random Forest classifier will also use the GINI Coefficient.
from sklearn.ensemble import RandomForestClassifier
randf = RandomForestClassifier(n_estimators=300)
randf.fit(X_train, y_train)
RandomForestClassifier(bootstrap=True, class_weight=None, criterion='gini',
max_depth=None, max_features='auto', max_leaf_nodes=None,
min_impurity_decrease=0.0, min_impurity_split=None,
min_samples_leaf=1, min_samples_split=2,
min_weight_fraction_leaf=0.0, n_estimators=300,
n_jobs=None, oob_score=False, random_state=None,
verbose=0, warm_start=False)
print(classification_report(y_train, randf.predict(X_train)))
precision recall f1-score support
0 1.00 1.00 1.00 18691
1 1.00 1.00 1.00 5309
accuracy 1.00 24000
macro avg 1.00 1.00 1.00 24000
weighted avg 1.00 1.00 1.00 24000
The training set has also been 100% correctly classified by the random forest model. Evaluating with the test set:
print(classification_report(y_test, randf.predict(X_test)))
precision recall f1-score support
0 0.84 0.94 0.89 4673
1 0.63 0.36 0.46 1327
accuracy 0.81 6000
macro avg 0.74 0.65 0.67 6000
weighted avg 0.79 0.81 0.79 6000
get_roc(randf, y_test, X_test, "Decision Tree (Random Forest)")
The random forest ensemble performs much better than the decision tree alone. The accuracy and AUROC are both superior to the decision tree alone.
xgBoost is short for "Extreme Gradient Boosting". It is a boosting ensemble method for decision trees. This means that the trees are trained consecutively, where each new tree added is trained to correct the error from the previous tree.
xgBoost uses the gradient descent algorithm that we learnt in BT2101 at each iteration to maximise the reduction in the error term. (More details? math?)
For consistency our xgBoost ensemble will use n_estimators = 300 as we have done for the random forest ensemble.
from sklearn.ensemble import GradientBoostingClassifier
xgb = GradientBoostingClassifier(n_estimators=300, max_depth = 4)
xgb.fit(X_train, y_train)
GradientBoostingClassifier(criterion='friedman_mse', init=None,
learning_rate=0.1, loss='deviance', max_depth=4,
max_features=None, max_leaf_nodes=None,
min_impurity_decrease=0.0, min_impurity_split=None,
min_samples_leaf=1, min_samples_split=2,
min_weight_fraction_leaf=0.0, n_estimators=300,
n_iter_no_change=None, presort='auto',
random_state=None, subsample=1.0, tol=0.0001,
validation_fraction=0.1, verbose=0,
warm_start=False)
print(classification_report(y_train, xgb.predict(X_train)))
precision recall f1-score support
0 0.86 0.96 0.91 18691
1 0.76 0.45 0.56 5309
accuracy 0.85 24000
macro avg 0.81 0.70 0.74 24000
weighted avg 0.84 0.85 0.83 24000
We observe that the xgBoost ensemble did not fully separate the data in the training set. (The default maximum depth is 3, so that might be a factor). Evaluating on the test set,
print(classification_report(y_test, xgb.predict(X_test)))
precision recall f1-score support
0 0.84 0.94 0.89 4673
1 0.63 0.35 0.45 1327
accuracy 0.81 6000
macro avg 0.74 0.65 0.67 6000
weighted avg 0.79 0.81 0.79 6000
get_roc(xgb, y_test, X_test, "Decision Tree (XGBoost)")
From the accuracy and AUROC, we observe that the XGBoost performs similarly to the random forest ensemble. It has a slight bump in AUROC at 0.76, but the accuracy is the same.
from sklearn import svm
#Linear classifier with cost function = 1
l_svm_clf = svm.SVC(C = 1, kernel = 'linear')
# the following line takes forever
l_svm_clf.fit(X_train, y_train)
r_svm_clf = svm.SVC(C= 1, kernel = 'rbf')